Question

cora says she doesn't need to know the y-intercept of a line to write its equation, just its slope and some other point on the line. Is she correct? Explain. If Cora is correct, explain how to find the equation of a line with a alope of -1/3 that includes the point (2,6).​

Answer 1

The equation of line with given slope that include given points is 3 y + x - 20 = 0

Explanation:

According to Cora , if we know the slope and points on a line then we can write the equation of a line .

Since , The equation of line in slope-intercept form is

y = m x + c

Where m is the slope of line , and if we know the points ( x , y ) which satisfy the line then constant term c can be get and the equation of line can be formed .

So , From the statement said above it is clear that she is correct .

Now , Again

Given as :

Slope of a line is m = -
`(1)/(3)`

That include points ( 2 , 6 )

Now from the equation of line as y = m x + c

∴ 6 = -
`(1)/(3)` ( 2 ) + c

Or, 6 = -
`(2)/(3)` + c

So , c = 6 +
`(2)/(3)`

or, c =
`(18 + 2)/(3)`

∴ c =
`(20)/(3)`

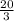
So, The equation of line can be written as

y = -
`(1)/(3)` x +
`(20)/(3)`

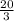
Or, 3 y = - x + 20

I.e 3 y + x - 20 = 0

Hence The equation of line with given slope that include given points is 3 y + x - 20 = 0 Answer