Answer:
0.36
Explanation:
Given, a circle with radius,
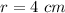
Area of circle =
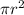
Substitute
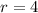
Area of whole circle
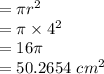
Square is inscribed in it whose each side is
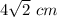
Area of square

We can see that area of the white circle
= area of the whole circle - area of square
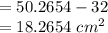
Probability of falling a random point within the white circle
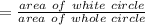
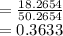
Rounding to nearest hundredth.
Probability of falling a random point within the white circle would be 0.36