Question

Please help, very urgent!

Answer 1

0.36

Explanation:

Given, a circle with radius,
`r=4 \ cm`

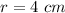
Area of circle =
`\pi r^2`

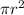
Substitute
`r=4`

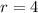
Area of whole circle
`=\pi r^2\\=\pi* 4^2\\=16\pi \\=50.2654\ cm^2`

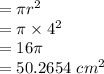
Square is inscribed in it whose each side is
`4√(2)\ cm`

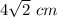
Area of square
`=side^2\\=(4√(2) )^2\\=16* 2\\=32 \ cm^2`

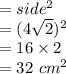
We can see that area of the white circle

= area of the whole circle - area of square

`=50.2654-32\\=18.2654 \ cm^2`

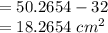
Probability of falling a random point within the white circle

`=(area\ of\ white\ circle)/(area\ of\ whole\ circle)`

`=(18.2654)/(50.2654) \\=0.3633`

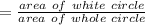
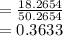
Rounding to nearest hundredth.

Probability of falling a random point within the white circle would be 0.36