Answer: 0.5898
Explanation:
Given : J.J. Redick of the Los Angeles Clippers had a free throw shooting percentage of 0.901 .
We assume that,
The probability that .J. Redick makes any given free throw =0.901 (1)
Free throws are independent.
So it is a binomial distribution .
Using binomial probability formula, the probability of getting success in x trials :
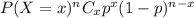
, where n= total trials
p= probability of getting in each trial.
Let x be binomial variable that represents the number of a=makes.
n= 14
p= 0.901 (from (1))
The probability that he makes at least 13 of them will be :-
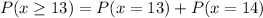
![=^(14)C_(13)(0.901)^(13)(1-0.901)^1+^(14)C_(14)(0.901)^(14)(1-0.901)^0\\\\=(14)(0.901)^(13)(0.099)+(1)(0.901)^(14)\ \ [\because\ ^nC_n=1\ \&\ ^nC_(n-1)=n ]\\\\\approx0.3574+0.2324=0.5898](https://img.qammunity.org/2020/formulas/mathematics/college/e023ozgqh0ec0zi168vi0xno9dpxrdvm5q.png)
∴ The required probability = 0.5898