Question

During the 2015-16 NBA season, J.J. Redick of the Los Angeles Clippers had a free throw shooting percentage of 0.901 . Assume that the probability J.J. Redick makes any given free throw is fixed at 0.901 , and that free throws are independent. Correct answer iconCorrect. (a) If J.J. Redick shoots 14 free throws in a game, what is the probability that he makes at least 13 of them? Round your answer to four decimal places.

Answer 1

Answer: 0.5898

Explanation:

Given : J.J. Redick of the Los Angeles Clippers had a free throw shooting percentage of 0.901 .

We assume that,

The probability that .J. Redick makes any given free throw =0.901 (1)

Free throws are independent.

So it is a binomial distribution .

Using binomial probability formula, the probability of getting success in x trials :

`P(X=x)^nC_xp^x(1-p)^(n-x)`

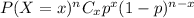
, where n= total trials

p= probability of getting in each trial.

Let x be binomial variable that represents the number of a=makes.

n= 14

p= 0.901 (from (1))

The probability that he makes at least 13 of them will be :-

`P(x\geq13)=P(x=13)+P(x=14)`

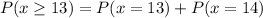
`=^(14)C_(13)(0.901)^(13)(1-0.901)^1+^(14)C_(14)(0.901)^(14)(1-0.901)^0\\\\=(14)(0.901)^(13)(0.099)+(1)(0.901)^(14)\ \ [\because\ ^nC_n=1\ \&\ ^nC_(n-1)=n ]\\\\\approx0.3574+0.2324=0.5898`

∴ The required probability = 0.5898