Answer:
a)At the 10% significance level, we fail to reject the null hypothesis.
b) P-value is ≈ 0.48
Explanation:
Let p be the proportion of the auditors agree with the statement "Cash flow is an important indicator of profitability."
Then,
 : p=0.5
: p=0.5
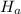 : p≠0.5
: p≠0.5
Test statistic can be calculated as:
z=
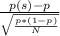 where
where
- p(s) is the sample proportion of the auditors agree with the statement. (
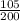 =0.525)
=0.525)
- p is the proportion assumed under null hypothesis. (0.5)
- N is the sample size (200)
Using these numbers we get:
z=
 ≈0,707
≈0,707
and p(z) is ≈ 0.48. Since 0.48>0.10, the result is not significant at 90% level. Therefore we fail to reject the null hypothesis.