Question

Near the center of our galaxy, hydrogen gas is moving directly away from us in its orbit about a black hole. The electromagnetic radiation we receive from this hydrogen gas has a Doppler-shifted wavelength of 1940 nm when it reaches earth. From experiments done on earth, we know the source wavelength is 1875 nm. What is the speed of the gas relative to earth?

Answer 1

To solve this problem it is necessary to apply the concept related to wavelength, specifically when the wavelength is observed from a source that is in motion to the observer.

By definition the wavelength is given defined by,

`\lambda_(obs) = \lambda_s \sqrt{(1+u/c)/(1-u/c)}`

Where

`\lambda_(obs)` = Observed wavelength

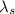`\lambda_s` = Wavelength of the source

c = Speed of light in vacuum

u = Relative velocity of the source to the observer

According to our data we have that the wavelength emitted from the galaxy is 1875nm which is equal to the wavelength from the source, while the wavelength from the observer is
`\lambda_(obs)=1945nm`

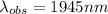
Therefore replacing in the previous equation we have,

`1945 = 1875 \sqrt{(1+(u)/(c) )/(1-(u)/(c) )}`

`\sqrt{(1+u/c)/(1-u/c)} = 1.03733`

`(1+(u)/(c) )/(1-(u)/(c) )=1.03733^2`

`1+(u)/(c) =1.03733^2*(1-(u)/(c) )`

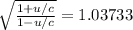
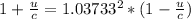
Solving for u,

`1+(u)/(c) =1.03733^2*(1-(u)/(c) )`

`1+(u)/(c) =1.03733^2-1.03733^2((u)/(c) )`

`(u)/(c) +1.03733^2(u)/(c) =1.03733^2-1`

`2.88595(u)/(c)=1.03733^2-1`

`(u)/(c) = (1.03733^2-1)/(2.88595)`

`u = (1.03733^2-1)/(2.88595)*c`

`u = 0.02635c`

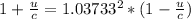
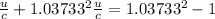
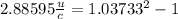
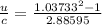
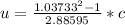
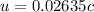
Therefore the speed of the gas relative to earth is 0.02635 times the speed of light.