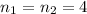Answer:
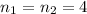
Explanation:
Given : Margin of error : E= 4.8
Confidence level : 92%
Significance level :
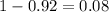
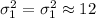
Two-tailed critical value :-
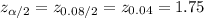
If we want to select independent random samples of equal size from the populations,
Formula for the sample size :
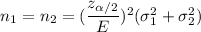
Then buy using given values , we have
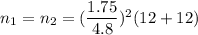
Simplify ,
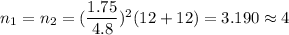 [Round to the next integer.]
[Round to the next integer.]
Hence, the The sample sizes should be: