Question

In a sample of 593 new websites registered on the Internet, 28 were anonymous (i.e., they shielded their name and contact information).

(a) Construct a 95 percent confidence interval for the proportion of all new websites that were anonymous. (Round your answers to 4 decimal places.)
(b) May normality of p be assumed?

Answer 1

a)
`0.0299\leq \widehat{p}\leq 0.0640`

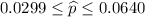
b)Yes

Explanation:

n = 593

x = 28

`\widehat{p}=(x)/(n)`

`\widehat{p}=(28)/(593)`

`\widehat{p}=0.047`

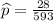
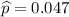
Confidence level = 95%

So,
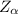`Z_\alpha` at 95% = 1.96

Formula of confidence interval of one sample proportion:

=
`\widehat{p}-Z_\alpha \sqrt{\frac{\widehat{p}(1-\widehat{p}}{n}}\leq \widehat{p}\leq \widehat{p}+Z_\alpha \sqrt{\frac{\widehat{p}(1-\widehat{p}}{n}}`

=
`0.047-(1.96)\sqrt{(0.047(1-0.047))/(593)}\leq \widehat{p}\leq 0.047+(1.96)\sqrt{(0.047(1-0.047)/(593)}`

=
`0.0299\leq \widehat{p}\leq 0.0640`

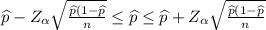
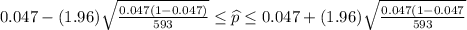
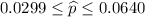
Hence a 95 percent confidence interval for the proportion of all new websites that were anonymous is
`0.0299\leq \widehat{p}\leq 0.0640`

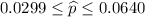
b) May normality of p be assumed?

Condition for normality : np>10 and np(1-p)>10.

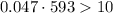`0.047\cdot593 >10` and
`0.047\cdot593(1-0.047)>10`

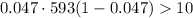
27.871 and 26.561063

Hence p is assumed to be normal since the condition is satisfied