Question

Air at 38°C and 97% relative humidity is to be cooled to 14°C and fed into a plant area at a rate of 510m3/min. (a) Calculate the rate (kg/min) at which water condenses. (b) Calculate the cooling requirement in tons 1 ton of cooling 12;000 Btu/h, assuming that the enthalpy of water vapor is that of saturated steam at the same temperature and the enthalpy of dry air is given by the expression

Answer 1

To develop the problem it is necessary to apply the concepts related to the ideal gas law, mass flow rate and total enthalpy.

The gas ideal law is given as,

`PV=mRT`

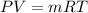
Where,

P = Pressure

V = Volume

m = mass

R = Gas Constant

T = Temperature

Our data are given by

`T_1 = 38\°C`

`T_2 = 14\°C`

`\eta = 97\%`

`\dot{v} = 510m^3/kg`

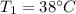
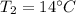
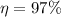
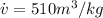
Note that the pressure to 38°C is 0.06626 bar

PART A) Using the ideal gas equation to calculate the mass flow,

`PV = mRT`

`\dot{m} = (PV)/(RT)`

`\dot{m} = (0.6626*10^(5)*510)/(287*311)`

`\dot{m} = 37.85kg/min`

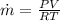
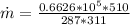
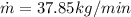
Therfore the mass flow rate at which water condenses, then

`\eta = \frac{\dot{m_v}}{\dot{m}}`

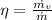
Re-arrange to find
`\dot{m_v}`

`\dot{m_v} = \eta*\dot{m}`

`\dot{m_v} = 0.97*37.85`

`\dot{m_v} = 36.72 kg/min`

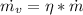
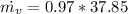
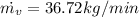
PART B) Enthalpy is given by definition as,

`H= H_a +H_v`

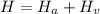
Where,

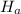`H_a`= Enthalpy of dry air

`H_v`= Enthalpy of water vapor

Replacing with our values we have that

`H=m*0.0291(38-25)+2500m_v`

`H = 37.85*0.0291(38-25)-2500*36.72`

`H = 91814.318kJ/min`

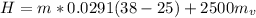
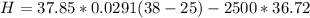
In the conversion system 1 ton is equal to 210kJ / min

`H = 91814.318kJ/min((1ton)/(210kJ/min))`

`H = 437.2tons`

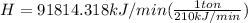
The cooling requeriment in tons of cooling is 437.2.