Question

1. In their entrepreneurship class, students are given two options for ways to earn a commission selling

cookies. For both options, students will be paid according to the number of boxes they are able to sell,
with commissions being paid only after all sales have ended. Students must commit to one commission
option before they begin selling.
Option 1: The commission for each box of cookies sold is 2 dollars.
Option 2: The commission will be based on the total number of boxes of cookies sold as follows: 2 cents
is the total commission if one box is sold, 4 cents is the commission if two boxes are sold,
8 cents if three boxes are sold, and so on, doubling the amount for each additional box sold.
(This option is based upon the total number of boxes sold and is paid on the total, not each
individual box.)
a. Define the variables and write function equations to model each option. Describe the domain for each function.
b. If Barbara thinks she can sell five boxes of cookies, should she choose Option 1 or 2?
c. Which option should she choose if she thinks she can sell ten boxes? Explain.
d. How many boxes of cookies would a student have to sell before Option 2 pays more than Option 1?
Show your work and verify your answer graphically.

Answer 1

a) x= number of boxes sold, y=commision

Option 1:

y=2x D=x ∈ Z ; x≥0

Option 2:

`y=\left \{ {{0;x=0} \atop {(2^(x))/(100):x>0}} \right.`

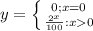
D=x ∈ Z ; x≥0

b) Option 1

c) Option 1

d) She has to sell 12 boxes of cookies so Option 2 pays more than Option 1

Explanation:

a)

In order to solve part a) of this problem, we must first determine which values will vary throughout this problem. We can see that the values that are variable are the number of boxes sold and the commision, so we can state that:

x= number of boxes sold, y=commision

Once our variables have been set, we can start building the equations for each of the options.

Option 1: The commission for each box of cookies sold is 2 dollars.

Since x is the number of boxes sold, we can multiply that by 2 dollars so our comission will be given by the following equation:

y=2x

since we cannot sell less than 0 boxes, then our domain must take this into account. So our domain will be:

D=x ∈ Z ; x≥0

this is, x can only get integer values that are greater than or equal to zero. The values x gets must be integer because there is no such thing as a fraction of a box. At least not for this problem.

Option 2: The commission will be based on the total number of boxes of cookies sold as follows: 2 cents

is the total commission if one box is sold, 4 cents is the commission if two boxes are sold,

8 cents if three boxes are sold, and so on, doubling the amount for each additional box sold.

Option 2 is describing an exponential function, because each time you sell one additional box, you need to multiply the previous commision by 2. Like this:

1 box y=2

2 boxes y=2*2=
`2^(2)`

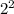
3 boxes y=2*2*2 =
`2^(3)`

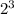
4 boxes y=2*2*2*2 =
`2^(4)`

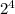
and so on, so the equation is:

`y=\left \{ {{0;x=0} \atop {(2^(x))/(100):x>0}} \right.`

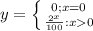
this is a piecewise defined function because if you don't sell any box, you will get 0 dollars as an answer. We need to divide
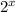`2^(x)` into 100 so our answer is given in dollars, since the 2 represents cents.

The domain for this function is the same as the domain for the first option, since it is not possible to sell less than 0 boxes of cookies, so the domain is:

D=x

b)

In order to solve part b we mus test each option for 5 boxes of cookies so we get:

Option 1:

y=2x

y=2(5)

y=$10

Option 2:

`y=(2^(x))/(100)`

`y=(2^(5))/(100)`

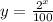
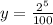
y=$0.32

so she should choose option 1 since whe will get $10 with that option compared to the 32 cents she would get with option 2.

c) The same procedure is followed in part c:

Option 1:

y=2x

y=2(10)

y=$20

Option 2:

`y=(2^(x))/(100)`

`y=(2^(10))/(100)`

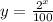
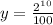
y=$10.24

so she should choose option 1 since whe will get $20 with that option compared to the $10.24 whe would get with option 2.

d) In order to solve this part you can build a chart comparing the different scenarios and pick the value for which you will get a greater commission for option 2 than that of option 1 (see picture attached) In the picture you will be able to see the graph as well where you can visualize what the behaviour of each option is. This is a step graph because you can only sell whole boxes.

According to the chart and the graph, you will have to sell 12 boxes to get a greater commision out of option 2 than of option 1.

Answer 2

C1(x)=2x C2(x)=(0,02)2^(x-1) with x integer biger than 1

Explanation:

a) here are two models, one for each option

C1(x)=2x

C2(x)=(0,02)2^(x-1) where x is an integer bigger or equal to 1, it is because our variable is the number of boxes . So the domain in both options is Inetegers positives.

b) She should choose C1 because C1(5) = 2*5 = 10 and C2(5)=(0,02)2^(4) = 0,32

c) it is the same case than b) C1(10) = 20 and C2(10)=(0,02)2^(9) = 10,24.

She should choose C1

d) if the student wants to earn more by choosing option 2, she must sell at least 12 boxes