Answer:
a) x= number of boxes sold, y=commision
Option 1:
y=2x D=x ∈ Z ; x≥0
Option 2:
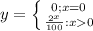
D=x ∈ Z ; x≥0
b) Option 1
c) Option 1
d) She has to sell 12 boxes of cookies so Option 2 pays more than Option 1
Explanation:
a)
In order to solve part a) of this problem, we must first determine which values will vary throughout this problem. We can see that the values that are variable are the number of boxes sold and the commision, so we can state that:
x= number of boxes sold, y=commision
Once our variables have been set, we can start building the equations for each of the options.
Option 1: The commission for each box of cookies sold is 2 dollars.
Since x is the number of boxes sold, we can multiply that by 2 dollars so our comission will be given by the following equation:
y=2x
since we cannot sell less than 0 boxes, then our domain must take this into account. So our domain will be:
D=x ∈ Z ; x≥0
this is, x can only get integer values that are greater than or equal to zero. The values x gets must be integer because there is no such thing as a fraction of a box. At least not for this problem.
Option 2: The commission will be based on the total number of boxes of cookies sold as follows: 2 cents
is the total commission if one box is sold, 4 cents is the commission if two boxes are sold,
8 cents if three boxes are sold, and so on, doubling the amount for each additional box sold.
Option 2 is describing an exponential function, because each time you sell one additional box, you need to multiply the previous commision by 2. Like this:
1 box y=2
2 boxes y=2*2=
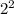
3 boxes y=2*2*2 =
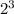
4 boxes y=2*2*2*2 =
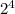
and so on, so the equation is:
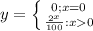
this is a piecewise defined function because if you don't sell any box, you will get 0 dollars as an answer. We need to divide
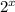 into 100 so our answer is given in dollars, since the 2 represents cents.
into 100 so our answer is given in dollars, since the 2 represents cents.
The domain for this function is the same as the domain for the first option, since it is not possible to sell less than 0 boxes of cookies, so the domain is:
D=x
b)
In order to solve part b we mus test each option for 5 boxes of cookies so we get:
Option 1:
y=2x
y=2(5)
y=$10
Option 2:
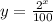
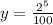
y=$0.32
so she should choose option 1 since whe will get $10 with that option compared to the 32 cents she would get with option 2.
c) The same procedure is followed in part c:
Option 1:
y=2x
y=2(10)
y=$20
Option 2:
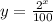
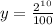
y=$10.24
so she should choose option 1 since whe will get $20 with that option compared to the $10.24 whe would get with option 2.
d) In order to solve this part you can build a chart comparing the different scenarios and pick the value for which you will get a greater commission for option 2 than that of option 1 (see picture attached) In the picture you will be able to see the graph as well where you can visualize what the behaviour of each option is. This is a step graph because you can only sell whole boxes.
According to the chart and the graph, you will have to sell 12 boxes to get a greater commision out of option 2 than of option 1.