Question

Calculate the mass of methane that must be burned to provide enough heat to convert 242.0 g of water at 26.0°C into steam at 101.0°C. (Assume that the H2O produced in the combustion reaction is steam rather than liquid water.)

Answer 1

Answer: The mass of methane burned is 12.4 grams.

Step-by-step explanation:

The chemical equation for the combustion of methane follows:

`CH_4(g)+2O_2(g)\rightarrow CO_2(g)+2H_2O(g)`

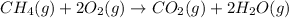
The equation for the enthalpy change of the above reaction is:

`\Delta H^o_(rxn)=[(1* \Delta H^o_f_((CO_2(g))))+(2* \Delta H^o_f_((H_2O(g))))]-[(1* \Delta H^o_f_((CH_4(g))))+(2* \Delta H^o_f_((O_2(g))))]`

We are given:

`\Delta H^o_f_((H_2O(g)))=-241.82kJ/mol\\\Delta H^o_f_((CO_2(g)))=-393.51kJ/mol\\\Delta H^o_f_((CH_4(g)))=-74.81kJ/mol\\\Delta H^o_f_(O_2)=0kJ/mol`

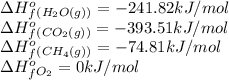
Putting values in above equation, we get:

`\Delta H^o_(rxn)=[(1* (-393.51))+(2* (-241.82))]-[(1* (-74.81))+(2* (0))]\\\\\Delta H^o_(rxn)=-802.34kJ`

The heat calculated above is the heat released for 1 mole of methane.

The process involved in this problem are:

`(1):H_2O(l)(26^oC)\rightarrow H_2O(l)(100^oC)\\\\(2):H_2O(l)(100^oC)\rightarrow H_2O(g)(100^oC)\\\\(3):H_2O(g)(100^oC)\rightarrow H_2O(g)(101^oC)`

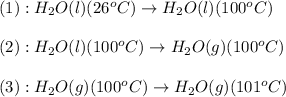
Now, we calculate the amount of heat released or absorbed in all the processes.

• For process 1:

`q_1=mC_p,l* (T_2-T_1)`

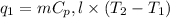
where,

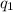`q_1` = amount of heat absorbed = ?

m = mass of water = 242.0 g

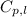`C_(p,l)` = specific heat of water = 4.18 J/g°C

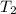`T_2` = final temperature =
`100^oC`

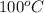
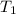`T_1` = initial temperature =
`26^oC`

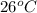
Putting all the values in above equation, we get:

`q_1=242.0g* 4.18J/g^oC* (100-(26))^oC=74855.44J`

• For process 2:

`q_2=m* L_v`

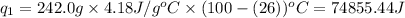
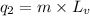
where,

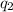`q_2` = amount of heat absorbed = ?

m = mass of water or steam = 242 g

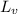`L_v` = latent heat of vaporization = 2257 J/g

Putting all the values in above equation, we get:

`q_2=242g* 2257J/g=546194J`

• For process 3:

`q_3=mC_p,g* (T_2-T_1)`

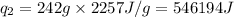
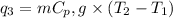
where,

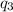`q_3` = amount of heat absorbed = ?

m = mass of steam = 242.0 g

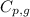`C_(p,g)` = specific heat of steam = 2.08 J/g°C

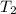`T_2` = final temperature =
`101^oC`

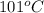
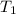`T_1` = initial temperature =
`100^oC`

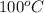
Putting all the values in above equation, we get:

`q_3=242.0g* 2.08J/g^oC* (101-(100))^oC=503.36J`

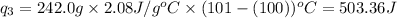
Total heat required =
`q_1+q_2+q_3=(74855.44+546194+503.36)=621552.8J=621.552kJ`

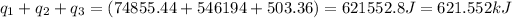
• To calculate the number of moles of methane, we apply unitary method:

When 802.34 kJ of heat is needed, the amount of methane combusted is 1 mole

So, when 621.552 kJ of heat is needed, the amount of methane combusted will be =
`(1)/(802.34)* 621.552=0.775mol`

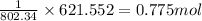
To calculate the number of moles, we use the equation:

`\text{Number of moles}=\frac{\text{Given mass}}{\text{Molar mass}}`

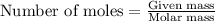
Molar mass of methane = 16 g/mol

Moles of methane = 0.775 moles

Putting values in above equation, we get:

`0.775mol=\frac{\text{Mass of methane}}{16g/mol}\\\\\text{Mass of methane}=(0.775mol* 16g/mol)=12.4g`

Hence, the mass of methane burned is 12.4 grams.