Answer:
The quantity of water drain after x min is 50
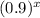
Explanation:
Given as :
Total capacity of rain barrel = 50 gallon
The rate of drain = 10 gallon per minutes
Let The quantity of water drain after x min = y
Now, according to question
The quantity of water drain after x min = Initial quantity of water ×
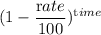
I.e The quantity of water drain after x min = 50 gallon ×
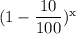
or, The quantity of water drain after x min = 50 gallon ×
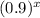
Hence the quantity of water drain after x min is 50
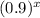 Answer
Answer