Question

A block oscillating on a spring has period T1 = 2.38s . Note that you do not know the value of either m or k, so do not assume any particular values for them. The required analysis involves thinking about ratios.

Part A: What is the period if the block's mass is doubled?
Part C: The value of the spring constant is quadrupled?
Part E:The oscillation amplitude is doubled while m and k are unchanged?

Answer 1

(a) T = 1.41 T₁ = 3.36 s

(b) T = 0.5 T₁ = 1.19 s

(e) The amplitude does not depend on the variation of m and k.

Step-by-step explanation:

The period of a block oscillating on a spring is giving by the next equation:

`T = 2\pi \sqrt(m)/(k)` (1)

where m: block's mass, and k: spring constant

(a) If the block's mass is doubled, the period will be:

`T = 2\pi \sqrt(2m)/(k) = \sqrt2 \cdot 2\pi \sqrt (m)/(k) = 1.41 \cdot T_(1) = 1.41 \cdot 2.38 s = 3.36 s`

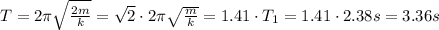
So, the period increase with the increase of the mass.

(c) If the value of the srping constant is quadrupled, from equation (1):

`T = 2\pi \sqrt(m)/(4k) = (1)/(\sqrt4) 2\pi \sqrt (m)/(k) = (1)/(2) T_(1) = 0.5 \cdot 2.38 s = 1.19 s`

The period decrease with the increase of the spring constant.

(e) The oscillation amplitude does not have a relation with m and k, and hence with the period, so if the m and k change or not, the amplitude is the same as the start.

Have a nice day!