Question

A student wanted to estimate the number of chocolate chips in a commercial brand of cookie. He sampled 100 cookies and found an average of 10.5 chips per cookie. If we assume the standard deviation is 8, what is a 99% confidence interval for the average number of chips per cookie?

A. (8.4,12.6)
B. (8.9,12.1)
C. (5.3,10.7)

Answer 1

Answer: A. (8.4,12.6)

Explanation:

Confidence interval
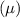`(\mu)` is given by :-

`\overline{x}\pm z_(\alpha/2)(\sigma)/(√(n))`

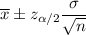
, where n is the sample size

`\sigma` = Population standard deviation.

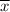`\overline{x}`= Sample mean

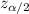`z_(\alpha/2)` = Two tailed z-value for significance level of
`\alpha`.

Given : Confidence level = 99% = 0.99

Significance level =
`\alpha=1-0.99=0.01`

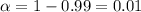
By standard normal z-value table ,

Two tailed z-value for Significance level of 0.01 :

`z_(\alpha/2)=z_(0.005)=2.576`

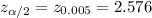
Also,

n=100

`\sigma= 8`

`\overline{x}=10.5`

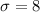
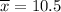
Then, the required 99% confidence interval for the average number
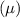`(\mu)` of chips per cookie :-

`10.5\pm (2.576)(8)/(√(100))\\\\ =10.5\pm 2.0608\\\\=(10.5-2.0608,\ 10.5+2.0608)=(8.4392,\ 12.5608)\approx(8.4,\ 12.6)`

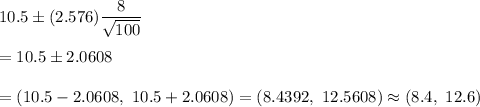
Hence, the 99% confidence interval for the average number of chips per cookie = (8.4,12.6)