Answer: A. (8.4,12.6)
Explanation:
Confidence interval
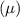 is given by :-
is given by :-
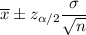
, where n is the sample size
 = Population standard deviation.
= Population standard deviation.
 = Sample mean
= Sample mean
 = Two tailed z-value for significance level of
= Two tailed z-value for significance level of
 .
.
Given : Confidence level = 99% = 0.99
Significance level =
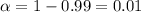
By standard normal z-value table ,
Two tailed z-value for Significance level of 0.01 :
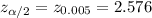
Also,
n=100
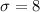
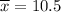
Then, the required 99% confidence interval for the average number
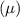 of chips per cookie :-
of chips per cookie :-

Hence, the 99% confidence interval for the average number of chips per cookie = (8.4,12.6)