Question

What is the magnitude of the maximum stress that exists at the tip of an internal crack having a radius of curvature of 3 × 10-4 mm (1.181 × 10-5 in.) and a crack length of 5.5 × 10-2 mm (2.165 × 10-3 in.) when a tensile stress of 150 MPa (21760 psi) is applied

Answer 1

maximum stress is 2872.28 MPa

Step-by-step explanation:

given data

radius of curvature = 3 ×
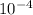`10^(-4)` mm

crack length = 5.5 ×
`10^(-2)` mm

tensile stress = 150 MPa

to find out

maximum stress

solution

we know that maximum stress formula that is express as

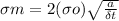`\sigma m = 2 ( \sigma o ) \sqrt{(a)/(\delta t)}` ......................1

here σo is applied stress and a is half of internal crack and t is radius of curvature of tip of internal crack

so put here all value in equation 1 we get

`\sigma m = 2 ( \sigma o) \sqrt{(a)/(\delta t)}`

`\sigma m = 2(150) \sqrt{ ((5.5*10^(-2))/(2))/(3*10^(-4))}`

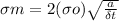
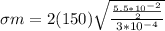
σm = 2872.28 MPa

so maximum stress is 2872.28 MPa