Answer:
Choice A. {
 }
}
Explanation:
Start by working on isolating the variable "x" in the inequality
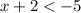 . We can do such by subtracting "2" from both sides:
. We can do such by subtracting "2" from both sides:
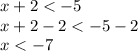
Therefore, we need to consider all those real values of the variable "x" which are strictly smaller than -7 (reside to the left of -7 on the number line).
Such set of x-values can be described in set notation (the notation suggested in your answer choices) specifying:
a) with the group symbols "{" and "}" the beginning and the end respectively of the set to be described,
b) with the expression "x |" we state: all those x-values such that,
c) with the symbols
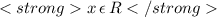 we state: x belongs to the set of Real (R) numbers,
we state: x belongs to the set of Real (R) numbers,
d) and finally the condition on the values allowed for the variable x: x < -7 (x values must be strictly smaller than "-7"