Question

Fyling against the wind, an airplane travels 4779 kilometers in 9 hours. Flying the same wind, the sampe plane travels 6060 kilometers in 6 hours. What is the rate of the plane still in the air abd what is the rate if the winf?

Answer 1

Rate of plane in still air: 770.5 km/hr

Rate of wind: 239.5 km/hr

Explanation:

Let x represent speed of plane in still air and w represent speed of wind.

Speed of plane with wind would be
`x+w`.

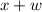Speed of plane against wind would be
`x-w`.

We will use following formula to solve our given orblem.

`\text{Distance}=\text{Speed}* \text{Time}`

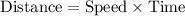
We have been given that flying against the wind, an airplane travels 4779 kilometers in 9 hours. We can represent this information in an equation as:

`9(x-w)=4779...(1)`

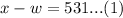`x-w=531...(1)` (Dividing by 9)

We are also told that flying with the wind, the same plane travels 6060 kilometers in 6 hours. We can represent this information in an equation as:

`6(x+w)=6060...(2)`

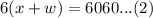
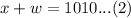`x+w=1010...(2)` (Dividing by 6)

Upon adding equation (1) and (2), we will get:

`(x-w)+(x+w)=531+1010`

`x-w+x+w=1541`

`2x=1541`

`(2x)/(2)=(1541)/(2)`

`x=770.5`

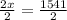
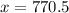
Therefore, the rate of the plane in still air is 770.5 kilometers per hour.

To find the rate of the wind, we will substitute
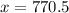`x=770.5` in equation (1) as:

`770.5-w=531`

`770.5-770.5-w=531-770.5`

`-w=-239.5`

`-1* -w=-1*-239.5`

`w=239.5`

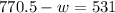
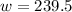
Therefore, the rate of the wind is 239.5 kilometers per hour.