Question

Hydrogen gas is used in a Carnot cycle having an efficiency of 60% with a low temperature of 300 K. During heat rejection, the pressure changes from 90 kPa to 120 kPa. Find the high- and low-temperature heat transfers and the net cycle work per unit mass of hy

Answer 1

q Low = 355.95 kJ/kg

q High = 889.9 kJ/kg

net cycle work = 533.9 kJ/kg

Step-by-step explanation:

given data

efficiency = 60%

temperature = 300 K

pressure changes = 90 kPa to 120 kPa

to find out

high and low temperature heat transfers and the net cycle work

solution

we know here that Carnot cycle efficiency is the maximum possible efficiency of the heat engines system between the specific temperature limit

so that efficiency we find here as high temperature is

efficiency =
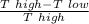`(T\ high - T\ low)/(T \ high)` ................1

we get

efficiency = 1 -
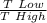`(T \ Low)/(T \ High)` .................2

put here value we get T high that is

0.6 = 1 -
`(300)/(T \ High)`

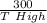
T high = 750 K

and now we get volume ratio for the heat transfer

t3 = T4 = T Low

so we get equation here as

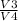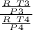`(V3)/(V4)` =
`((R\ T3)/(P3))/((R\ T4)/(P4))` .........................3

`(P4)/(P3) =(120)/(90)` = 1.33

we know that value of R from A5 Table that is

R = 4.1243

so efficiency will be here

q Low = R ×T Low × ln
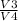`(V3)/(V4)` .................4

put the value we get

q Low = 4.1243 × 300 × 1.33

q Low = 355.95 kJ/kg

and

q High =
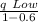`(q\ Low)/(1-0.6)` ...................5

q High =
`(355.95)/(1-0.6)`

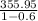
q High = 889.9 kJ/kg

so we can say that net cycle work = net transfer

net cycle work = q High - q Low .....................6

net cycle work = 889.9 - 355.95

net cycle work = 533.9 kJ/kg