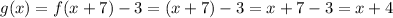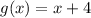Answer:
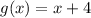
Explanation:
Given
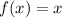
 shifted 7 units left and 3 units down
shifted 7 units left and 3 units down
Translation Rules:
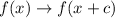
If
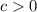 the function shifts
the function shifts
 units to the left.
units to the left.
If
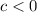 the function shifts
the function shifts
 units to the right.
units to the right.
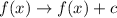
If
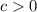 the function shifts
the function shifts
 units to the up.
units to the up.
If
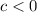 the function shifts
the function shifts
 units to the down.
units to the down.
Applying the rules to

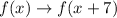 [7 units left]
[7 units left]
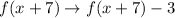 [3 units down]
[3 units down]
∴