Question

Select the correct answer.

A six-sided fair die and an eight-sided fair die are rolled together. What is the probability of getting numbers whose sum is a multiple of 3?

Answer 1

C. 1/3

Explanation:

Answer 2

Answer:
`(1)/(3)`

Explanation:

Favorable outcomes (sum is a multiple of 3): (1,2) , (1, 5), (1,8), (2,1) , (2,4), (2,7) , (3, 3), (3, 6), (4, 2), (4, 5) , (4, 8), (5,1), (5, 4), (5, 7), (6,3), (6, 6).

Number of favorable outcomes (sum is a multiple of 3): 16

Total outcomes = Total outcomes of 6-sided die x Total outcomes of 8-sided die=6 × 8 = 48

Then , the probability of getting numbers whose sum is a multiple of 3:

`=\frac{\text{favorable outcomes}}{\text{total outcomes}}\\\\=(16)/(48)=(1)/(3)`

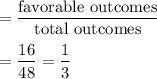
Hence, the required probability =
`(1)/(3)`