Answer:
c) 6x + y = -52 is required equation perpendicular to the given equation.
Explanation:
If the equation is of the form : y = mx + C.
Here m = slope of the equation.
Two equations are said to be perpendicular if the product of their respective slopes is -1.
Here, equation 1 : -x + 6y = -12
or, 6y = -12 + x
or, y = (x/6) - 2
⇒Slope of line 1 = (1/6)
Now, for equation 2 to be perpendicular:
Check for each equation:
a. x + 6y = -67 ⇒ 6y = -67 - x
or, y = (-x/6) - (67/6) ⇒Slope of line 2 = (-1/6)
but
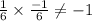
b. x - 6y = -52 ⇒ -6y = -52 - x
or, y = (x/6) + (52/6) ⇒Slope of line 2 = (1/6)
but
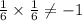
c. 6x + y = -52
or, y =y = -52 - 6x ⇒Slope of line 2 = (-6)
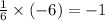
Hence, 6x + y = -52 is required equation 2.
d. 6x - y = 52 ⇒ -y = 52 - 6x
or, y = 6x - 52 ⇒Slope of line 2 = (6)
but
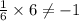
Hence, 6x + y = -52 is the only required equation .