Question

Which equation has a graph that is perpendicular to the graph of -x + 6y = -12?

a. x + 6y = -67
b. x - 6y = -52
c. 6x + y = -52
d. 6x - y = 52

Answer 1

C

Explanation:

Let
`l_(1)` be the equation of the line with slope
`m_(1)` and let
`l_(2)` be the equation of the line with slope
`m_(2)`.

As we know,for two lines
`l_(1)` and
`l_(2)` to be perpendicular,

`m_(1)* m_(2) =-1`

In the given problem,slope of given line=
`m_(1)`=
`(-6)/(-1)=6`

For option a,slope =
`m_(2)`
`=(-6)/(1) =-6`

In this case,
`m_(1)* m_(2)=6* -6=-36`

So,option a is incorrect.

For option b,slope =
`m_(2)`
`=(6)/(1) =6`

In this case,
`m_(1)* m_(2)=6* 6=36`

So,option b is incorrect.

For option c,slope =
`m_(2)`
`=(-1)/(6) =(-1)/(6)`

In this case,
`m_(1)* m_(2)=6* (-1)/(6)=-1`

So,option c is correct.

For option d,slope =
`m_(2)`
`=(1)/(6) =(1)/(6)`

In this case,
`m_(1)* m_(2)=6* (1)/(6)=1`

So,option d is incorrect.

Answer 2

c) 6x + y = -52 is required equation perpendicular to the given equation.

Explanation:

If the equation is of the form : y = mx + C.

Here m = slope of the equation.

Two equations are said to be perpendicular if the product of their respective slopes is -1.

Here, equation 1 : -x + 6y = -12

or, 6y = -12 + x

or, y = (x/6) - 2

⇒Slope of line 1 = (1/6)

Now, for equation 2 to be perpendicular:

Check for each equation:

a. x + 6y = -67 ⇒ 6y = -67 - x

or, y = (-x/6) - (67/6) ⇒Slope of line 2 = (-1/6)

but
`(1)/(6) * (-1)/(6)  \\eq -1`

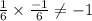
b. x - 6y = -52 ⇒ -6y = -52 - x

or, y = (x/6) + (52/6) ⇒Slope of line 2 = (1/6)

but
`(1)/(6) * (1)/(6)  \\eq -1`

c. 6x + y = -52

or, y =y = -52 - 6x ⇒Slope of line 2 = (-6)

`(1)/(6) * (-6)  =  -1`

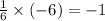
Hence, 6x + y = -52 is required equation 2.

d. 6x - y = 52 ⇒ -y = 52 - 6x

or, y = 6x - 52 ⇒Slope of line 2 = (6)

but
`(1)/(6) * 6  \\eq -1`

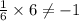
Hence, 6x + y = -52 is the only required equation .