Question

Solve 3 ^ (x - 8) = 8 for x using the change of base formula logb y = (log y)/(log b)

Answer 1

x = 3 (Log 2 base 3) + 8

Explanation:

3^(x - 8) = 8

Take the log of both side

Log 3^(x - 8) = Log 8

Recall:

log a^b = b log a

Log 3^(x - 8) = Log 8

(x - 8) Log 3 = Log 8

Divide both side by log 3

x - 8 = Log 8 / log 3

Recall:

8 = 2^3

x - 8 = Log 8 / log 3

x - 8 = Log 2^3 / log 3

x - 8 = 3 Log 2 / log 3

Recall:

logb y = log y / log b

log y / log b = logb y

x - 8 = 3 Log 2 / log 3

x - 8 = 3 Log3 2

Add 8 to both side

x = 3 Log3 2 + 8

x = 3 (Log 2 base 3) + 8

Answer 2

`x=3\log_3 (2) +8`

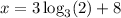
Explanation:

Here we are using power rule first.

Power rule = The logarithm of an exponential number is the exponent times the logarithm of the base
`[log(a)^(b)=b* log(a)]`.

For the function given.

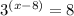`3^((x-8)) = 8`,using log function both sides.

`(x-8)log(3)=log(8)`

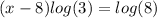
Now,

`(x-8)=(log(8))/(log(3))`

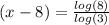
Adding
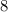`8` both sides.

`x=(log(8))/(log(2)) +8`

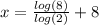
And we know that
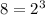`8=2^(3)` so we can further write
`log(8)=log(2^(3))=3log(2)`

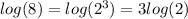
Then we have
`x=(3\log(2))/(\log 3) +8`.

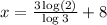Now, using change of base formula:

`(\log y)/(\log b)=\log_b y`

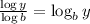
So,
`(\log 2)/(\log 3)=\log_3 2`

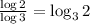
Our final answer is
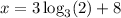`x=3\log_3 (2) +8`.