Answer:
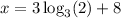
Explanation:
Here we are using power rule first.
Power rule = The logarithm of an exponential number is the exponent times the logarithm of the base
![[log(a)^(b)=b* log(a)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/vyj6yvcybld9y4rdn5pb4mp4slvlxk2q7g.png) .
.
For the function given.
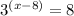 ,using log function both sides.
,using log function both sides.

Now,

Adding
 both sides.
both sides.

And we know that
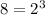 so we can further write
so we can further write
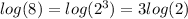
Then we have
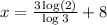 .
.
Now, using change of base formula:
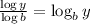
So,
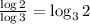
Our final answer is
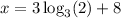 .
.