Answer:
6 if 7 doesnt divide n, 42 otherwise. The only possible options are those 2.
Explanation:
I will find the possible answers, since no options were given
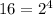 , thus, 16 only has 2 as a prime divisor. We conclude that n = 4*k, with k an odd number. On the other hand,
, thus, 16 only has 2 as a prime divisor. We conclude that n = 4*k, with k an odd number. On the other hand,
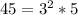 , since the greatest factor between n and 45 is 3, then 5 is not a divisor of n, and n has the form 3*j, with j not a multiple of 3. Since 3 and 4 doesnt have common primes as factors, then j = 4*l, with l odd.
, since the greatest factor between n and 45 is 3, then 5 is not a divisor of n, and n has the form 3*j, with j not a multiple of 3. Since 3 and 4 doesnt have common primes as factors, then j = 4*l, with l odd.
Thus n = 12 * j, with j a number that satisfies:
- 3 is not a divisor of j
- 2 is not a divisor of j
- 5 is not a divisor of j
Note that
 . 12 is not factor of 210, but 6 is. j doesnt have any prime divisor in common with 210, with the exception, maybe, of 7. So the greatest common factor of them is 1 or 7, depending on weather 7 divides j (or equivalently, n) or not. Therefore, the greatest common factor of n and 210 could be 6, if 7 does not divide n, or 6*7 = 42, if 7 divides n.
. 12 is not factor of 210, but 6 is. j doesnt have any prime divisor in common with 210, with the exception, maybe, of 7. So the greatest common factor of them is 1 or 7, depending on weather 7 divides j (or equivalently, n) or not. Therefore, the greatest common factor of n and 210 could be 6, if 7 does not divide n, or 6*7 = 42, if 7 divides n.
I hope that works for you!