Answer:
A)
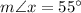
B) Angle relationship used to find
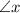 was alternate interior angles of a traversal between two parallel lines
was alternate interior angles of a traversal between two parallel lines
Explanation:
Given :
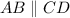
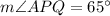
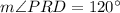
To find measure of
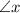 .
.
Part A
From the figure we can say:
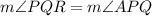 [Alternate interior angles are congruent]
[Alternate interior angles are congruent]
∴
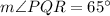 [By substitution ∵
[By substitution ∵
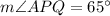 ]
]
For Δ PQR
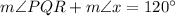 [Sum of two interior angles of a triangle is equal to the opposite exterior angle]
[Sum of two interior angles of a triangle is equal to the opposite exterior angle]
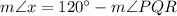 [By subtraction property of equality]
[By subtraction property of equality]
 [By substitution ∵
[By substitution ∵
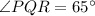
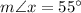
Part B:
We used the angle relationship of alternate interior angles of traversal
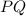 between two parallel lines
between two parallel lines
 to find measure one angle of the Δ PQR which in turn helped us to find the measure of other angle of triangle which is
to find measure one angle of the Δ PQR which in turn helped us to find the measure of other angle of triangle which is
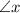 as the two angles found are opposite to the exterior angle that is =120°
as the two angles found are opposite to the exterior angle that is =120°
Relation used:
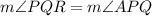 [Alternate interior angles are congruent]
[Alternate interior angles are congruent]
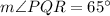 [By substitution ∵
[By substitution ∵
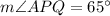 ]
]