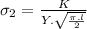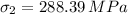Answer:
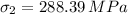
Step-by-step explanation:
Given:
Strain fracture toughness,
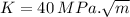
maximum internal crack length in first case,

stress level in the first case,
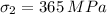
maximum internal crack length in second case,
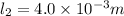
stress level in the second case,
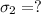
So, now we require a factor given as:
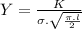
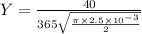
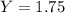
Now,