Answer:
The length of line segment AC = 6.44 inches
Explanation:
Given as :
ABC is a right angle triangle, right angle at c
So , ∠ ACB = 90°
And ∠ ABC = 40°
So, ∠ BCA = 180° - ( ∠ ACB + ∠ ABC )
Or, ∠ BCA = 180° - ( 90° + 40° )
I.e ∠ BCA = 50°
The length of Hypotenuse = 10 inches
The length of AC = Perpendicular = b
The length of CB = Base = a
∵ This is a right angled Triangle , then
Hypotenuse² = Perpendicular² + Base²
Or, 10² = AC² + BC²
Or, 10² = b² + a² ...1
Now, From triangle ABC
Tan 50° =
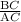
I.e 1.19 =
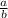
So, a = 1.19 b
From eq 1
10² = b² + (1.19 b)²
Or, 100 = 2.41 b²
so, b² =
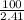 = 41.49
= 41.49
∴ b =
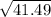 = 6.44 inches
= 6.44 inches
And a = 1.19 × 6.44 = 7.66 inches
Hence The length of line segment AC = 6.44 inches Answer