Answer:
The slope of AB is -7/4, the slope of BC is 1/7 , the slope of CD is 5/3, and the slope of AD is 2. So, Quadrilateral ABCD is neither a parallelogram nor a trapezoid because neither pair of opposite sides are parallel.
Explanation:
Since, a quadrilateral having,
One pair of parallel opposite sides is Trapezoid,
While, having two pair of parallel opposite sides is parallelogram.
Since, the slope of a line segment having the end points
 and
and
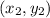 is,
is,

Here, the vertices of the quadrilateral ABCD are A(0, −4) , B(−4, 3) , C(3, 4) , and D(6, −1),
Slope of AB =
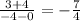
Slope of BC =
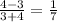
Slope of CD =
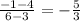
Slope of AD =
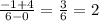
Hence, Quadrilateral ABCD is neither a parallelogram nor a trapezoid because neither pair of opposite sides are parallel.