Answer:
The initial temperature of the object was 37.6
Explanation:
we have
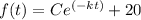
where
f(t) represent the temperature of the object in degree Celsius
t is the time in minutes
Find the value of the constant C
we have the ordered pair (4,35)
substitute in the equation and solve for C
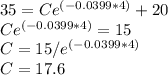
Find the initial value of the object
we know that
The initial temperature is the value of f(t) when the value of t is equal to zero
so
For t=0
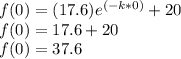
therefore
The initial temperature of the object was 37.6 (I not include units)