Question

The Ace Novelty company produces two souvenirs: Type A and Type B. The number of Type A souvenirs, x, and the number of Type B souvenirs, y, that the company can produce weekly are related by the equation 2x2 + y − 4 = 0, where x and y are measured in units of a thousand. The profits for a Type A souvenir and a Type B souvenir are $4 and $2, respectively. How many of each type of souvenirs should the company produce to maximize its profit?

Answer 1

500 type A; 3500 type B

Explanation:

The method of Lagrange multipliers can solve this quickly. For objective function f(x, y) and constraint function g(x, y)=0 we can set the partial derivatives of the Lagrangian to zero to find the values of the variables at the extreme of interest.

These functions are ...

`f(x,y)=4x+2y\\g(x,y)=2x^2+y-4`

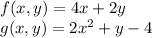
The Lagrangian is ...

`\mathcal{L}(x,y,\lambda)=f(x,y)+\lambda g(x,y)\\\\\text{and the partial derivatives are ...}\\\\\frac{\partial \mathcal{L}}{\partial x}=(\partial f)/(\partial x)+\lambda(\partial g)/(\partial x)=4+\lambda (4x)=0\ \implies\ x=(-1)/(\lambda)\\\\\frac{\partial \mathcal{L}}{\partial y}=(\partial f)/(\partial y)+\lambda(\partial g)/(\partial y)=2+\lambda (1)=0\ \implies\ \lambda=-2`

`\frac{\partial\mathcal{L}}{\partial\lambda}=(\partial f)/(\partial\lambda)+\lambda(\partial g)/(\partial\lambda)=0+2x^2+y-4=0\ \implies\ y=4-2x^2\\\\\text{We know $\lambda$, so we can find x and y:}\\\\x=(-1)/(-2)=0.5\\\\y=4-2\cdot 0.5^2=3.5`

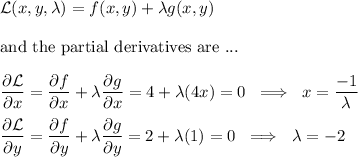
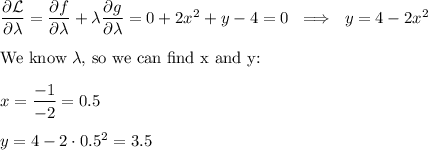
Since x and y are in thousands, maximum profit is to be had when the company produces ...

500 Type A souvenirs, and 3500 Type B souvenirs