Answer:
500 type A; 3500 type B
Explanation:
The method of Lagrange multipliers can solve this quickly. For objective function f(x, y) and constraint function g(x, y)=0 we can set the partial derivatives of the Lagrangian to zero to find the values of the variables at the extreme of interest.
These functions are ...
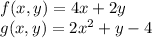
The Lagrangian is ...
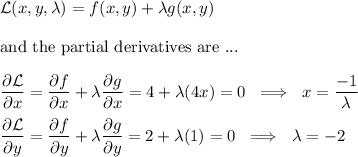

Since x and y are in thousands, maximum profit is to be had when the company produces ...
500 Type A souvenirs, and 3500 Type B souvenirs