Answer:
Option A
Solution:
As per the question:
Initially, voltage is
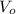
Current is 'I' A
Length of the wire is L
Now,
We know that:
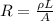 (1)
(1)
where
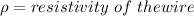
A = Cross sectional area of the wire
From eqn (1), if other things are taken to be constant, then
R ∝ L (2)
Thus
When the wire is cut into two reducing the length to
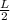
Resistance, R' =
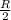
Now, when these wires are connected as described, the connection is in parallel, therefore, the equivalent resistance of the two wires:
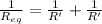
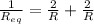
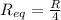
Now, from Ohm's law:
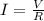
Since, according to the question voltage
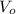 is constant, thus
is constant, thus
I ∝
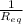
I ∝
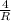
Thus
I becomes 4I