Answer:
The speed of plane in still air is 330 kmph
Explanation:
Given as :
The distance cover against the wind = 600 km
The time taken against the wind = 2 hours
The distance cover with the wind = 600 km
The time taken with the wind = ( 1 +
 ) hours
) hours
=
 hours
hours
Let The speed against the wind = x - y kmph
The speed with the wind = x + y kmph
where x is the speed of plane in still air
And y is the speed of wind
So , Speed =
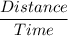
Or, x - y =
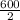 = 300 ......A
= 300 ......A
And x + y =

Or , x + y = 360 .......B
From eq A and B
( x + y ) - ( x - y ) = 360 - 300
Or, 2 y = 60
∴ y =
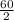 = 30 kmph
= 30 kmph
And x = 360 - 30 = 330 kmph
Hence The speed of plane in still air is 330 kmph Answer