Answer with Explanation:
We are given that
Current in conductor=I=4.99 A (-x direction)
Magnetic field=B=
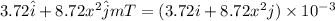
(1mT=
 )
)
x(in m) and B (in mT)
Length of conductor is given in negative x- direction
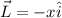
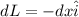
Force on current carrying conductor is given by
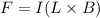
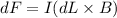
Integrating on both sides then we get
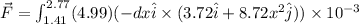
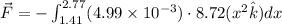 (
(
![\vec{F}=-(4.99* 10^(-3)* 8.72)[\frac{x^3\hat{k}}{3}]^(2.77)_(1.41)](https://img.qammunity.org/2020/formulas/physics/college/vb694lf0b5avl96n5n0rimh8aszd92vrs4.png)
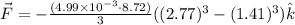
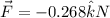
a. x- component of force=0
b.y- component of force=0
c.z- component of force=-0.268 N