8 unit tiles should be added
Explanation:
Function given is
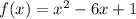 . We wish to add more unit tiles to the function so that it becomes a complete square.
. We wish to add more unit tiles to the function so that it becomes a complete square.
Since the given function is of order 2, the side of the square will be order 1. Let us assume a general order 1 expression
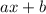 to be the side of the square.
to be the side of the square.
As the function forms the square after adding some
 unit tiles,
unit tiles,
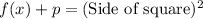
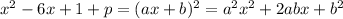
From comparision,
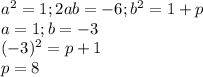
∴ 8 more unit tiles are required to complete the square.