Question

electric generator consists of a circular coil of wire of radius 4.0×10−2 m , with 20 turns. The coil is located between the poles of a permanent magnet in a uniform magnetic field, of magnitude 5.0×10−2 T . The B field is orientated perpendicular to the axis of rotation. The ends of the coil are connected via sliding contacts across a resistor of resistance 1.5 Ω. The peak current measured through the resistor is 3.0×10−3 A . Part A What is the angular frequency ω at which the coil is rotating

Answer 1

0.89524 rad/s

Step-by-step explanation:

N = Number of turns = 20

r = Radius of coil of wire =
`4* 10^(-2)\ m`

B = Magnetic field =
`5* 10^(-2)\ T`

I = Current =
`3* 10^(-3)\ A`

A = Area of coil =
`\pi r^2`

R = Resistance =
`1.5\ \Omega`

Maximum current in a generator is given by

`I=(NBA\omega)/(R)\\\Rightarrow \omega=(IR)/(NBA)\\\Rightarrow \omega=(IR)/(NB\pi r^2)\\\Rightarrow \omega=(3* 10^(-3)* 1.5)/(20* 5* 10^(-2)* \pi* (4* 10^(-2))^2)\\\Rightarrow \omega=0.89524\ rad/s`

The angular frequency is 0.89524 rad/s

Answer 2

w = 0.8957 rad/sec

Step-by-step explanation:

we know that Maximum current in coil can be calculated as

`I = (NBAw)/(R)`

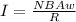
where N represent number of turn = 20

B = magnetic field
`=  5 * 10^(-2) T`

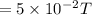
R is resistance = 1.5 ohm

`I = 3.0* 10^(-3) A`

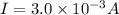
A = area
`= \pi r^2`

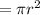
solving for angular frequency w

`w  = (I R)/(NB \pi r^2)`

`w = (3.0* 10^(-3) * 1.5)/(20* 5* 10^(-2) \pi *(4* 10^(-2))^2)`

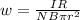
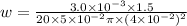
w = 0.8957 rad/sec