Answer:
w = 0.8957 rad/sec
Step-by-step explanation:
we know that Maximum current in coil can be calculated as
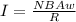
where N represent number of turn = 20
B = magnetic field
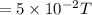
R is resistance = 1.5 ohm
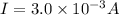
A = area
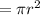
solving for angular frequency w
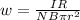

w = 0.8957 rad/sec