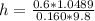Question

A Frisbee (160 g, 25 cm in diameter) spins a rate of 300 rpm with its center balanced on a fingertip. What is the rotational kinetic energy of the Frisbee if the disc has 70% of its mass on the outer edge (basically a thin ring 25-cm in diameter) and the remaining 30% is a nearly flat disk 25-cm in diameterthis is word for word what the question says.the final answer is 1.05 J ; 40.1cm -> i dont know how they came to that answer, and why there is an x value in cmAlthough I provided the answer, please show me how to come up with it

Answer 1

To solve this exercise it is necessary to take into account the concepts related to Moment of Inertia and Kinetic Energy.

The rotational kinetic energy is given by the function

`KE_r = (1)/(2) I\omega^2`

Where,

I = Inertia moment

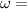`\omega =`Angular velocity

The moment of inertia must be divided by the mass fractions located outside and inside.

The general formula for the disk is,

`I = mR^2`

However the Moment of Inertia Total must be written as a sum between the Inertia outside and Inside,

`I_t = I_o+I_i`

`I_t = (0.70m R^2) + ((0.30m R^2)/(2))`

`I_t = 0.70 mR^2 + 0.15 mR^2`

`I = 0.85 MR^2`

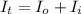
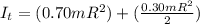
Therefore replacing with our values we have that for a mass of 160g and radius of 25/2cm

`I = 0.85 * 0.160 * 0.125^2`

`I = 2.125*10^(-3)kgm^2`

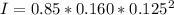
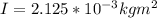
At the same time we calculate the angular velocity given as

`\omega = 300 rpm = 300 * (2pi)/(60)`

`\omega = 31.42 rad/s`

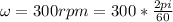
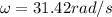
Applying the equation for Rotational Kinetic Energy we can calculate the total value given as,

`KE_r = (1)/(2) I \omega^2`

`KE_r = (1)/(2)(2.125*10^(-3)) (31.42^2)`

`KE_r = 1.0489J`

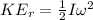
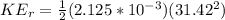
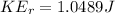
The problem also say that the rotational kinetic energy is converted to gravitational potential energy with an efficiency of 60%, then

`PE = 60\% KE_r`

`mgh = 0.6*1.0489J`

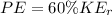
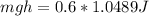
Solving for h,

`h= (0.6*1.0489)/(0.160 *9.8)`

`h = 0.4013m \approx 40cm`