Question

Drew is going to his friend’s house after school and wants to track how far he walks. He first walks 1.25 miles north, then 0.75 miles east, and finally 0.25 miles south to get to his friend’s house. When Drew leaves, his friend tells him that there’s a shortcut through the park to walk straight back to his house, 1.25 miles.

a rectangular shape of park split into a standard triangle and a polygon

How many miles does Drew save by taking the shortcut instead of retracing the same route back home?

Answer 1

Drew saves a distance of
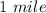`1\ mile` by taking the shortcut.

Explanation:

Here is an image of the routes.

We have drawn it assigning the signs NSEW where N=North,S=South ,E=East and W=West.

Now the total distance covered by Drew = OA+AB+BC
`=(1.25+0.75+0.25)=2.25\ miles`

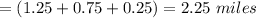
We see by joining C with O it has a shortcut.

And it forms a right angled triangle.

`\triangle ODC` ,
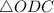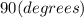`90(degrees)` at D.

By using Pythagoras theorem we can find the shortcut distance.

OC is the hypotenuse and
`OC=√(1^2+0.75^2) = 1.25\ miles`

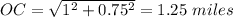
So Drew saves
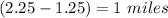`(2.25-1.25)=1\ miles` of distance following the advice of his friend and opting for the shortcut route.