Question

You have a spool of copper wire 4.82 mm in diameter and a power supply. You decide to wrap the wire tightly around a soda can that is 12.0 cm long and has a diameter of 6.50 cm, forming a coil, and then slide the wire coil off the can to form a solenoid. If the power supply can produce a maximum current of 230 A in the coil, what is the maximum magnetic field you would expect to produce in this solenoid? Assume the resistivity of copper is 1.68 ✕ 10−8 Ω · m. (Enter the magnitude.)

Answer 1

To solve the problem it is necessary to have the concepts of the magnetic field in a toroid.

A magnetic field is a vector field that describes the magnetic influence of electric charges in relative motion and magnetized materials.

By definition the magnetic field is given by the equation,

`B=(\mu_0 NI)/(2\pi r)`

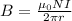
Where,

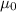`\mu_0` = Permeability constant

N = Number of loops

I = Current

r = Radius

According to the given data we have that the length is 120mm and the thickness of the copper wire is 4.82mm.

In this way the number of turns N would be

`N=(120mm)/(4.82mm)`

`N = 24.89 \approx 25 turns`

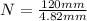
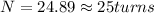
On the other hand to find the internal radius, we know that:

`2\pi r_i = 12cm`

`r_i= (12)/(2\pi)`

`r_i= 1.91cm`

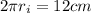
Therefore the total diameter of the soda would be

`r= r_i+r_o = 1.91+6.5=8.51cm`

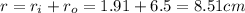
Applying the concept related to magnetic field you have to for the internal part:

`B_i=(\mu_0 NI)/(2\pi r_i)`

`B_i=((4\pi*10^(-7)) (25)(230))/(2\pi (1.91*10^(-2)))`

`B_i = 0.060T`

The smallest magnetic field would be on the outside given by,

`B_o=(\mu_0 NI)/(2\pi r)`

`B_o=((4\pi*10^(-7)) (25)(230))/(2\pi 8.51)`

`B_o = 0.0136T`

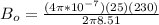
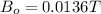
Therefore the maximum magnetic field is 0.06T.