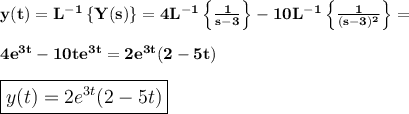Question

) Use the Laplace transform to solve the following initial value problem: y′′−6y′+9y=0y(0)=4,y′(0)=2 Using Y for the Laplace transform of y(t), i.e., Y=L{y(t)}, find the equation you get by taking the Laplace transform of the differential equation (s^2-6s+9)Y-4s+22 equation editorEquation Editor =0 Solve for Y(s)= (4s-22)/(s^2-6s+9) equation editorEquation Editor write the above answer in its partial fraction decomposition, Y(s)=As+a+B(s+a)2 Y(s)= equation editorEquation Editor + equation editorEquation Editor Now, by inverting the transform, find y(t)= equation editorEquation Editor .

Answer 1

`y(t)=2e^(3t)(2-5t)`

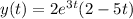
Explanation:

Let Y(s) be the Laplace transform Y=L{y(t)} of y(t)

Applying the Laplace transform to both sides of the differential equation and using the linearity of the transform, we get

L{y'' - 6y' + 9y} = L{0} = 0

(*) L{y''} - 6L{y'} + 9L{y} = 0 ; y(0)=4, y′(0)=2

Using the theorem of the Laplace transform for derivatives, we know that:

`\large\bf L\left\{y''\right\}=s^2Y(s)-sy(0)-y'(0)\\\\L\left\{y'\right\}=sY(s)-y(0)`

Replacing the initial values y(0)=4, y′(0)=2 we obtain

`\large\bf L\left\{y''\right\}=s^2Y(s)-4s-2\\\\L\left\{y'\right\}=sY(s)-4`

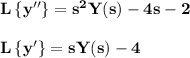
and our differential equation (*) gets transformed in the algebraic equation

`\large\bf s^2Y(s)-4s-2-6(sY(s)-4)+9Y(s)=0`

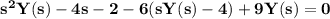
Solving for Y(s) we get

`\large\bf s^2Y(s)-4s-2-6(sY(s)-4)+9Y(s)=0\Rightarrow (s^2-6s+9)Y(s)-4s+22=0\Rightarrow\\\\\Rightarrow Y(s)=(4s-22)/(s^2-6s+9)`

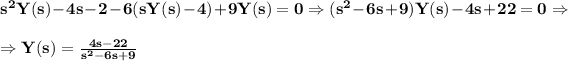
Now, we brake down the rational expression of Y(s) into partial fractions

`\large\bf (4s-22)/(s^2-6s+9)=(4s-22)/((s-3)^2)=(A)/(s-3)+(B)/((s-3)^2)`

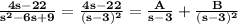
The numerator of the addition at the right must be equal to 4s-22, so

A(s - 3) + B = 4s - 22

As - 3A + B = 4s - 22

we deduct from here

A = 4 and -3A + B = -22, so

A = 4 and B = -22 + 12 = -10

It means that

`\large\bf (4s-22)/(s^2-6s+9)=(4)/(s-3)-(10)/((s-3)^2)`

and

`\large\bf Y(s)=(4)/(s-3)-(10)/((s-3)^2)`

By taking the inverse Laplace transform on both sides and using the linearity of the inverse:

`\large\bf y(t)=L^(-1)\left\{Y(s)\right\}=4L^(-1)\left\{(1)/(s-3)\right\}-10L^(-1)\left\{(1)/((s-3)^2)\right\}`

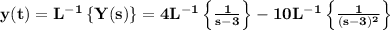
we know that

`\large\bf L^(-1)\left\{(1)/(s-3)\right\}=e^(3t)`

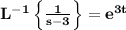
and for the first translation property of the inverse Laplace transform

`\large\bf L^(-1)\left\{(1)/((s-3)^2)\right\}=e^(3t)L^(-1)\left\{(1)/(s^2)\right\}=e^(3t)t=te^(3t)`

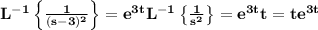
and the solution of our differential equation is

`\large\bf y(t)=L^(-1)\left\{Y(s)\right\}=4L^(-1)\left\{(1)/(s-3)\right\}-10L^(-1)\left\{(1)/((s-3)^2)\right\}=\\\\4e^(3t)-10te^(3t)=2e^(3t)(2-5t)\\\\\boxed{y(t)=2e^(3t)(2-5t)}`