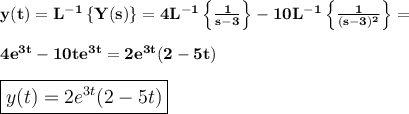Answer:
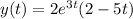
Explanation:
Let Y(s) be the Laplace transform Y=L{y(t)} of y(t)
Applying the Laplace transform to both sides of the differential equation and using the linearity of the transform, we get
L{y'' - 6y' + 9y} = L{0} = 0
(*) L{y''} - 6L{y'} + 9L{y} = 0 ; y(0)=4, y′(0)=2
Using the theorem of the Laplace transform for derivatives, we know that:
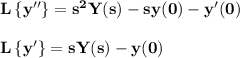
Replacing the initial values y(0)=4, y′(0)=2 we obtain
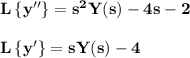
and our differential equation (*) gets transformed in the algebraic equation
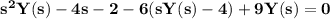
Solving for Y(s) we get
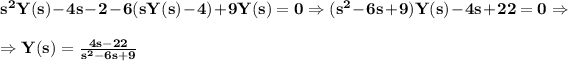
Now, we brake down the rational expression of Y(s) into partial fractions
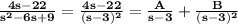
The numerator of the addition at the right must be equal to 4s-22, so
A(s - 3) + B = 4s - 22
As - 3A + B = 4s - 22
we deduct from here
A = 4 and -3A + B = -22, so
A = 4 and B = -22 + 12 = -10
It means that
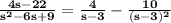
and
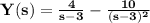
By taking the inverse Laplace transform on both sides and using the linearity of the inverse:
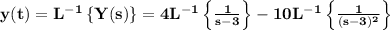
we know that
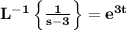
and for the first translation property of the inverse Laplace transform
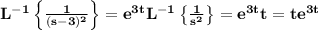
and the solution of our differential equation is