Step-by-step explanation:
Energy of the electron in the ground state,
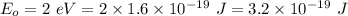
(a) The energy of the electron is square well is given by :
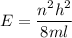
Where
l is the width of the box
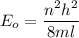



(b) For first excited state, n = 2
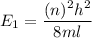
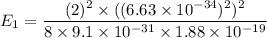
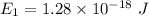
(c) Let n is the value of quantum number of the excited state. Again using this formula as :
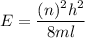
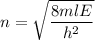
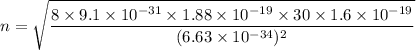
n = 3.86
or
n = 4
Hence, this is the required solution.