Question

An electron in a box is in the ground state with energy 2.0 eV. (a) Find the width of the box. (b) How much energy is needed to excite the electron to its first excited state? (c) If the electron makes a transition from an excited state to the ground state with the simultaneous emission of 30.0-eV photon, find the quantum number of the excited state?

Answer 1

Step-by-step explanation:

Energy of the electron in the ground state,
`E_o=2\ eV=2* 1.6* 10^(-19)\ J=3.2* 10^(-19)\ J`

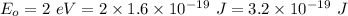
(a) The energy of the electron is square well is given by :

`E=(n^2h^2)/(8ml)`

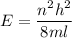
Where

l is the width of the box

`E_o=(n^2h^2)/(8ml)`

`l=(n^2h^2)/(8mE_o)`

`l=((1)^2* (6.63* 10^(-34))^2)/(8* 9.1* 10^(-31)* 3.2* 10^(-19))`

`l=1.88*10^(-19)\ m`

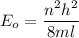
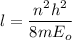
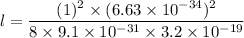
(b) For first excited state, n = 2

`E_1=((n)^2h^2)/(8ml)`

`E_1=((2)^2* ((6.63* 10^(-34))^2)^2)/(8* 9.1* 10^(-31)* 1.88*10^(-19))`

`E_1=1.28* 10^(-18)\ J`

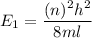
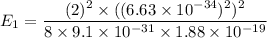
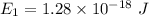
(c) Let n is the value of quantum number of the excited state. Again using this formula as :

`E=((n)^2h^2)/(8ml)`

`n=\sqrt{(8ml E)/(h^2)}`

`n=\sqrt{(8 * 9.1* 10^(-31)* 1.88 * 10^(-19) * 30* 1.6* 10^(-19))/((6.63* 10^(-34))^2)}`

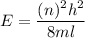
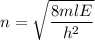
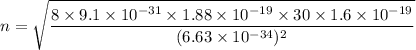
n = 3.86

or

n = 4

Hence, this is the required solution.