Answer:
The angular frequency at which the coil is rotating is 17.9rad/s
Step-by-step explanation:
To solve the exercise it is necessary to take into account the concepts related to the magnetic field in a wire, Farada's law and Ohm's Law.
The rotational induced voltage is defined by
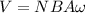
Where,
N = Number of loops
A = Cross-sectional area
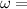 angular velocity
angular velocity
B = Magnetic Field
For Ohm's law we have,
V = IR
Where,
I= Current
V = Voltage
R = Resistance
Equation both equations,
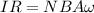
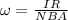
Our values are given as,
N = 20
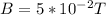
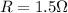
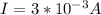
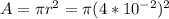
Replacing the values we have,
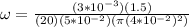
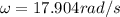
Therefore the angular frequency at which the coil is rotating is 17.9rad/s