Question

An electric generator consists of a circular coil of wire of radius 4.0×10−2 m , with 20 turns. The coil is located between the poles of a permanent magnet in a uniform magnetic field, of magnitude 5.0×10−2 T . The B field is orientated perpendicular to the axis of rotation. The ends of the coil are connected via sliding contacts across a resistor of resistance 1.5 Ω. The peak current measured through the resistor is 3.0×10−3 A. What is the angular frequency ω at which the coil is rotating? in rad/s to two sig figs.

Answer 1

The angular frequency at which the coil is rotating is 17.9rad/s

Step-by-step explanation:

To solve the exercise it is necessary to take into account the concepts related to the magnetic field in a wire, Farada's law and Ohm's Law.

The rotational induced voltage is defined by

`V = NBA\omega`

Where,

N = Number of loops

A = Cross-sectional area

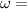`\omega =`angular velocity

B = Magnetic Field

For Ohm's law we have,

V = IR

Where,

I= Current

V = Voltage

R = Resistance

Equation both equations,

`IR = NBA\omega`

`\omega = (IR)/(NBA)`

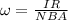
Our values are given as,

N = 20

`B =5*10^(-2)T`

`R = 1.5\Omega`

`I = 3*10^(-3)A`

`A = \pi r^2= \pi (4*10^(-2))^2`

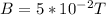
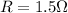
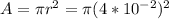
Replacing the values we have,

`\omega = ((3*10^(-3))(1.5))/((20)(5*10^(-2))( \pi (4*10^(-2))^2))`

`\omega = 17.904rad/s`

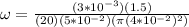
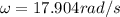
Therefore the angular frequency at which the coil is rotating is 17.9rad/s